PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning
Por um escritor misterioso
Last updated 04 novembro 2024
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://d3i71xaburhd42.cloudfront.net/a0174a41c7d682aeb1d7e7fa1fbd2404e037a638/11-Figure8.1-1.png)
It is shown that the CG method with variable preconditioning under this assumption may not give improvement, compared to the steepest descent (SD) method, and a new elegant geometric proof of the SD convergence rate bound is given. We analyze the conjugate gradient (CG) method with variable preconditioning for solving a linear system with a real symmetric positive definite (SPD) matrix of coefficients $A$. We assume that the preconditioner is SPD on each step, and that the condition number of the preconditioned system matrix is bounded above by a constant independent of the step number. We show that the CG method with variable preconditioning under this assumption may not give improvement, compared to the steepest descent (SD) method. We describe the basic theory of CG methods with variable preconditioning with the emphasis on “worst case” scenarios, and provide complete proofs of all facts not available in the literature. We give a new elegant geometric proof of the SD convergence rate bound. Our numerical experiments, comparing the preconditioned SD and CG methods, not only support and illustrate our theoretical findings, but also reveal two surprising and potentially practically important effects. First, we analyze variable preconditioning in the form of inner-outer iterations. In previous such tests, the unpreconditioned CG inner iterations are applied to an artificial system with some fixed preconditioner as a matrix of coefficients. We test a different scenario, where the unpreconditioned CG inner iterations solve linear systems with the original system matrix $A$. We demonstrate that the CG-SD inner-outer iterations perform as well as the CG-CG inner-outer iterations in these tests. Second, we compare the CG methods using a two-grid preconditioning with fixed and randomly chosen coarse grids, and observe that the fixed preconditioner method is twice as slow as the method with random preconditioning.
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i1.rgstatic.net/publication/259976327_The_Steepest_Descent_Method_for_Linear_Minimax_Problems/links/02e7e52ed337b7c1ad000000/largepreview.png)
PDF) The Steepest Descent Method for Linear Minimax Problems
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i.ytimg.com/vi/zjzOYL4fhrQ/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AHUBoAC4AOKAgwIABABGHIgNyg-MA8=&rs=AOn4CLCrZjsBGBt2aQ1ILO_N3dNsba6p5A)
Preconditioned Conjugate Gradient Descent (ILU)
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://media.springernature.com/lw685/springer-static/image/chp%3A10.1007%2F978-3-030-36468-7_13/MediaObjects/472714_1_En_13_Fig1_HTML.png)
The Conjugate Gradient Method
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i1.rgstatic.net/publication/305111885_Novel_preconditioners_based_on_quasi-Newton_updates_for_nonlinear_conjugate_gradient_methods/links/59f65e0a458515547c230ff0/largepreview.png)
PDF) Novel preconditioners based on quasi–Newton updates for
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://wikimedia.org/api/rest_v1/media/math/render/svg/1526b952271de30f00e5b91abf3a44337dfaef97)
Conjugate gradient method - Wikipedia
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://d3i71xaburhd42.cloudfront.net/70000f7791ab8519429ce939bc897738a05939c3/23-Figure16-1.png)
PDF] An Introduction to the Conjugate Gradient Method Without the
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://d3i71xaburhd42.cloudfront.net/70000f7791ab8519429ce939bc897738a05939c3/26-Figure19-1.png)
PDF] An Introduction to the Conjugate Gradient Method Without the
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://media.springernature.com/lw685/springer-static/image/chp%3A10.1007%2F978-3-030-36468-7_13/MediaObjects/472714_1_En_13_Fig3_HTML.png)
The Conjugate Gradient Method
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://onlinelibrary.wiley.com/cms/asset/47a49746-686b-4b96-ada3-9f0535d25edc/gamm.v43.4.cover.jpg?trick=1700487419750)
Preconditioners for Krylov subspace methods: An overview - Pearson
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://image.slidesharecdn.com/141206labmeetinglinearsystemspublic-141216055915-conversion-gate02/85/solving-poisson-equation-using-conjugate-gradient-methodand-its-implementation-1-320.jpg?cb=1666790430)
Solving Poisson Equation using Conjugate Gradient Method and its
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i.ytimg.com/vi/9LT-i5LiK7A/maxresdefault.jpg)
Preconditioning: Gradient Descent, Conjugate Gradients and SESOP
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i1.rgstatic.net/publication/2128371_Steepest_Descent_and_Conjugate_Gradient_Methods_with_Variable_Preconditioning/links/54124a4d0cf2fa878ad39ab6/largepreview.png)
PDF) Steepest Descent and Conjugate Gradient Methods with Variable
Recomendado para você
-
 Introduction to Method of Steepest Descent04 novembro 2024
Introduction to Method of Steepest Descent04 novembro 2024 -
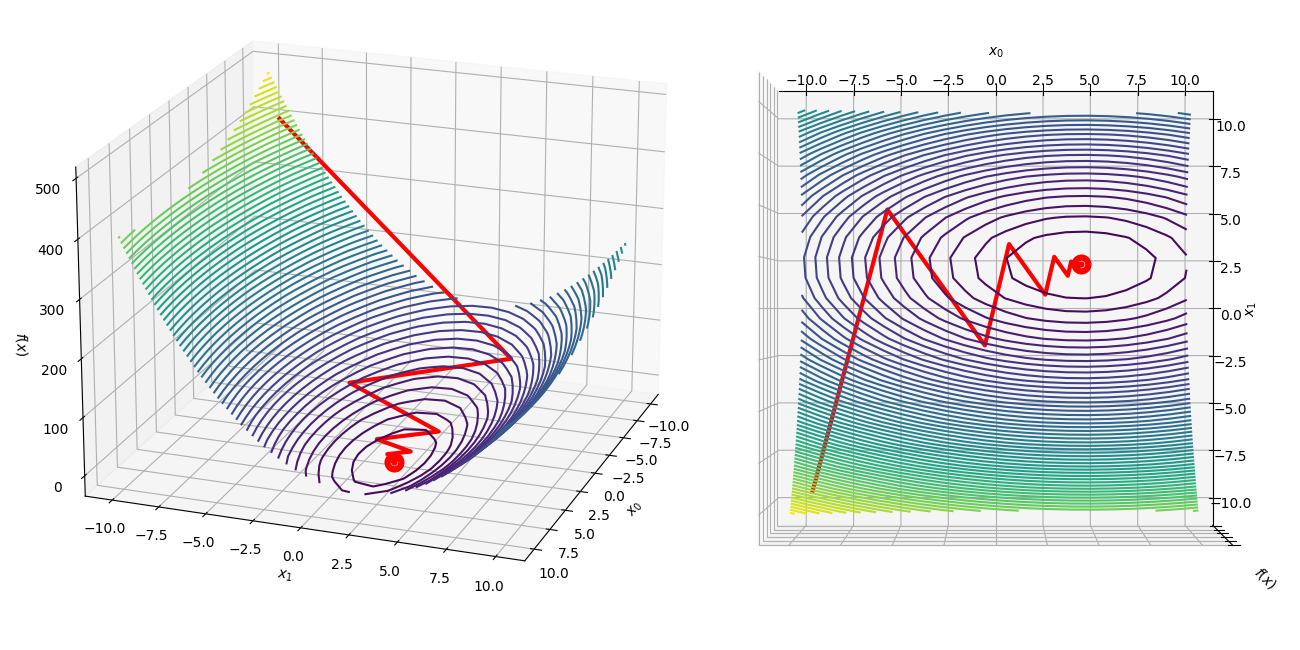 Implementing the Steepest Descent Algorithm in Python from Scratch, by Nicolo Cosimo Albanese04 novembro 2024
Implementing the Steepest Descent Algorithm in Python from Scratch, by Nicolo Cosimo Albanese04 novembro 2024 -
 A Steepest Descent Method for Set Optimization Problems with Set-Valued Mappings of Finite Cardinality04 novembro 2024
A Steepest Descent Method for Set Optimization Problems with Set-Valued Mappings of Finite Cardinality04 novembro 2024 -
 Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings04 novembro 2024
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings04 novembro 2024 -
 optimization - How to show that the method of steepest descent does not converge in a finite number of steps? - Mathematics Stack Exchange04 novembro 2024
optimization - How to show that the method of steepest descent does not converge in a finite number of steps? - Mathematics Stack Exchange04 novembro 2024 -
 Curves of Steepest Descent for 3D Functions - Wolfram Demonstrations Project04 novembro 2024
Curves of Steepest Descent for 3D Functions - Wolfram Demonstrations Project04 novembro 2024 -
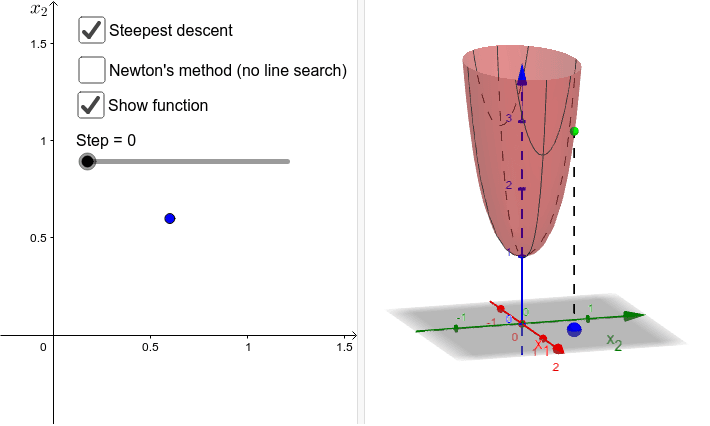 Steepest descent vs gradient method – GeoGebra04 novembro 2024
Steepest descent vs gradient method – GeoGebra04 novembro 2024 -
 I want to find x solution using Steepest Descent by Python. But when I was running it, it said invalid syntax at def. what should I fix about? - Stack Overflow04 novembro 2024
I want to find x solution using Steepest Descent by Python. But when I was running it, it said invalid syntax at def. what should I fix about? - Stack Overflow04 novembro 2024 -
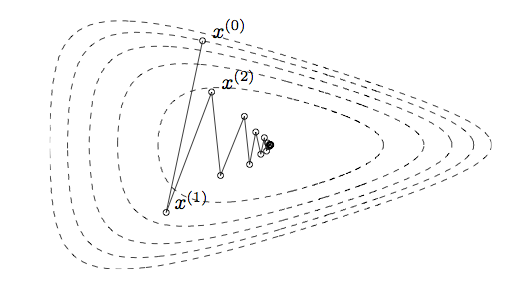 gradient-descent-backtracking.png04 novembro 2024
gradient-descent-backtracking.png04 novembro 2024 -
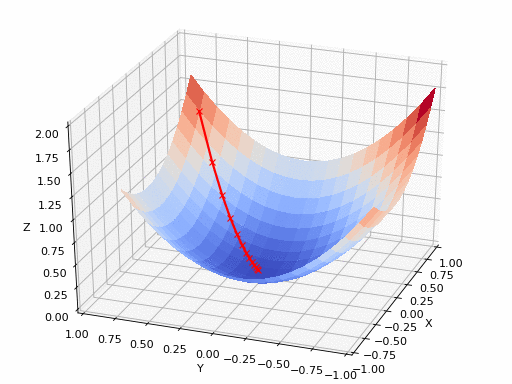 Gradient Descent - AI Wiki04 novembro 2024
Gradient Descent - AI Wiki04 novembro 2024
você pode gostar
-
 Miraculous: As Aventuras de Ladybug – O Filme - Filme 202304 novembro 2024
Miraculous: As Aventuras de Ladybug – O Filme - Filme 202304 novembro 2024 -
 Vasto Lorde, Kurosaki Ichigo, Bleach, anime vectors, anime, horns - wallpaper #117728 (4156x2342px) on04 novembro 2024
Vasto Lorde, Kurosaki Ichigo, Bleach, anime vectors, anime, horns - wallpaper #117728 (4156x2342px) on04 novembro 2024 -
Futebol de Botão - Izinhlelo zokusebenza ku-Google Play04 novembro 2024
-
 Resident Evil 2 Remake: 10 Things You Need To Know04 novembro 2024
Resident Evil 2 Remake: 10 Things You Need To Know04 novembro 2024 -
![no spoilers] I remade the Dalish Origin art with my gal Mahariel : r/ dragonage](https://preview.redd.it/no-spoilers-i-remade-the-dalish-origin-art-with-my-gal-v0-7i4j921ysisa1.jpg?width=2048&format=pjpg&auto=webp&s=76c59d397ce1c125055b1e532b7105e2818431d1) no spoilers] I remade the Dalish Origin art with my gal Mahariel : r/ dragonage04 novembro 2024
no spoilers] I remade the Dalish Origin art with my gal Mahariel : r/ dragonage04 novembro 2024 -
 KIT VESTIDO XADREZ ROSA MODELO PATRICINHA RODADO - Pityticos Moda04 novembro 2024
KIT VESTIDO XADREZ ROSA MODELO PATRICINHA RODADO - Pityticos Moda04 novembro 2024 -
 Sonic The Hedgehog 3 Poster, Sonic The Hedgehog 3 Movie Poster, sold by Flurry Quixotic | SKU 12745872 | Printerval04 novembro 2024
Sonic The Hedgehog 3 Poster, Sonic The Hedgehog 3 Movie Poster, sold by Flurry Quixotic | SKU 12745872 | Printerval04 novembro 2024 -
 Razer Atheris Review04 novembro 2024
Razer Atheris Review04 novembro 2024 -
 The Eminence in Shadow season 2 to release both English subbed and dubbed on its premiere04 novembro 2024
The Eminence in Shadow season 2 to release both English subbed and dubbed on its premiere04 novembro 2024 -
 Dragon Ball Super Dublado! Dragon Ball Oficial™ Amino04 novembro 2024
Dragon Ball Super Dublado! Dragon Ball Oficial™ Amino04 novembro 2024